Math Department Colloquium “Quantifying Gerrymandering: A mathematician goes to court” scheduled November 8 at 4pm

Thursday, November 8, from 4:00–5:00, in SAS 1102.
This will be preceded by a tea at 3:15 in SAS 4104.
SPEAKER: Jonathan Mattingly, Duke University
TITLE: Quantifying Gerrymandering: A mathematician goes to court
ABSTRACT: In October 2017, I found myself testify for hours in a Federal court. I had not been arrested. Rather I was attempting to quantifying gerrymandering using analysis which grew from asking if a surprising 2012 election was in fact surprising. It hinged on probing the geopolitical structure of North Carolina using a Markov Chain Monte Carlo algorithm. I will start at the beginning and describe the mathematical ideas involved in our analysis. Our mathematical analysis was one of the main pieced of testimony used by the Court to conclude in Common Cause v Rucho that the congressional districts used from 2016 to the present in North Carolina were unconstitutional as they were a political gerrymander. This cause is currently headed to the Supreme Court of the United States.
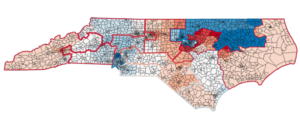
I will also explain the current state of the court cases and rulings and their implications for the mathematics needed moving forward. As time permits I will also discuss some open mathematical problems and issues which come from these investigations.
The talk will be largely assessable to undergraduates. If fact, this project began as a sequence of undergraduate research projects and undergraduates continue to be involved to this day
BIO:
Jonathan Christopher Mattingly grew up in Charlotte, NC where he attended Irwin Ave elementary and Charlotte Country Day. He graduated from the NC School of Science and Mathematics and received a BS is Applied Mathematics with a concentration in physics from Yale University. After two years abroad with a year spent at ENS Lyon studying nonlinear and statistical physics on a Rotary Fellowship, he returned to the US to attend Princeton University where he obtained a PhD in Applied and Computational Mathematics in 1998. After 4 years as a Szego assistant professor at Stanford University and a year as a member of the IAS in Princeton, he moved to Duke in 2003. He is currently a Professor of Mathematics and of Statistical Science.
His expertise is in the longtime behavior of stochastic system including randomly forced fluid dynamics, turbulence, stochastic algorithms used in molecular dynamics and Bayesian sampling, and stochasticity in biochemical networks.
He is the recipient of a Sloan Fellowship and a PECASE CAREER award. He is also a fellow of the IMS and the AMS. He received the “Defender of Democracy Award” from the National Common Cause for his work in Quantifying Gerrymandering.
- Categories:


