
- This event has passed.
Shahar Kovalsky, Duke University, Planar surface embeddings and non-convex harmonic maps
October 22, 2019 | 3:00 pm - 4:00 pm EDT
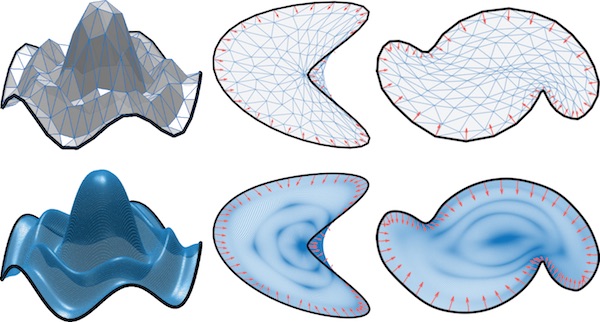 Mappings between domains are among the most basic and versatile tools used in the computational analysis and manipulation of shapes. Their applications range from animation in computer graphics to analysis of anatomical variation and anomaly detection in medicine and biology.
Mappings between domains are among the most basic and versatile tools used in the computational analysis and manipulation of shapes. Their applications range from animation in computer graphics to analysis of anatomical variation and anomaly detection in medicine and biology.
My talk will start with a brief overview of discrete computational shape mapping, surface parameterization (flattening), and their applications. I will then discuss invertibility, an often desirable property of mappings, and present an optimization approach for efficiently computing invertible surface maps. With large-scale problems in mind, we will focus on Tutte’s embedding theorem and its continuous counterpart, the Rado-Kneser-Choquet theorem: they assert that planar harmonic maps (solutions of Laplace’s equation) with convex boundary conditions are invertible. Finally, we will see that convexity, a key ingredient of both theorems, can be replaced with a novel, less restrictive and geometrically intuitive condition, thus extending these theorems to the case of harmonic maps onto non-convex domains.