
- This event has passed.
Symbolic Computation: Parker Edwards, University of Notre Dame, Feature Sizes and Bottlenecks for Algebraic Manifolds
October 13, 2022 | 4:30 pm - 5:30 pm EDT
In computational topology and geometry, theoretical guarantees for algorithms often take the following form: Start with a finite sample of points from a subspace of  . If the sample is “dense enough” with respect to the subspace, then the algorithm outputs a quantity of interest for the subspace, for example its Betti numbers. The quantities associated to a subspace which determine how dense of a sample is necessary are well studied by computational geometers: the reach, local feature size, and weak feature size of a subspace.
. If the sample is “dense enough” with respect to the subspace, then the algorithm outputs a quantity of interest for the subspace, for example its Betti numbers. The quantities associated to a subspace which determine how dense of a sample is necessary are well studied by computational geometers: the reach, local feature size, and weak feature size of a subspace.
Rather than a set of points, an algebraic space 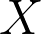 is specified by a system of polynomial equations. To apply the above methods in a theoretically sound way, one must use the space’s defining equations both to compute its feature sizes and subsequently a dense point sample from the space. In this talk, I will discuss new theory and algorithms to compute feature sizes of algebraic manifolds using numerical algebraic geometry methods, and exhibit several example computations, including from a robotics application. The corresponding theory investigates the differential critical point/value theory of, the distance-to-X function
is specified by a system of polynomial equations. To apply the above methods in a theoretically sound way, one must use the space’s defining equations both to compute its feature sizes and subsequently a dense point sample from the space. In this talk, I will discuss new theory and algorithms to compute feature sizes of algebraic manifolds using numerical algebraic geometry methods, and exhibit several example computations, including from a robotics application. The corresponding theory investigates the differential critical point/value theory of, the distance-to-X function  , from an algebraic geometry perspective.
, from an algebraic geometry perspective.
This is joint with Sandra Di Rocco, David Eklund, Oliver Gäfvert, and Jonathan Hauenstein.
Meeting ID: 997 2519 0147
Passcode: 032625